Kinetic theory of kids July 23, 2010
Posted by mareserinitatis in humor, science.Tags: children, humor, physics, science
trackback
It’s always fun to bring my kids to play when visiting with my scientist and engineer friends. Inevitably, the most haggard of us will comment on “how much energy they have!”
My response for the past few years has been, “Oh, we have the same amount of energy as we do, they just have less mass.” This has elicited laughter, groans, and, more often than I care to admit, blank stares.
Therefore, I have decided it is time to proffer a full explanation as more than once I have wanted to say, “Go look it up on my blog.”
Energy, as you may know, has an amorphous quality about it: it makes things move, makes them hot, makes them roll downhill, but it’s hard to define. It’s just one of those things things that we assign a number to and use it to do calculations.
The most important things about energy are that 1 – it is conserved because 2 – it can change from one form to another. As an example, a ball rolling across the floor will slow down because it’s transferring the motion from its energy into heat. The energy doesn’t go away (is conserved) but simply changes to a different form.
Fortunately, for this explanation, we’ll only deal with one form of energy: kinetic, or energy due to an object’s motion. It turns out that kinetic energy is proportional to the object’s mass and the square of its velocity. Specifically,
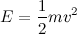
As I said, energy is conserved. This means it can’t go away but just can be transformed into another type of energy. However, I half jokingly assert that kids have the same amount of energy as adults, so I’m corrupting the meaning. But, moving along, we’ll assume this means that we can set the energy of an adult equal to that of a child. We’ll use the subscript A for adult and C for a child. (The use of the subscript k would be for kid, but that leaves a certain amount of ambiguity as to whether the topic of the post is human children or goats.)
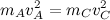
If we want to know how fast a child should move relative to an adult, we can rearrange the terms to get:
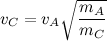
In words, the root of the ratio of the adult mass to child’s mass will give the factor describing how much faster the child moves than the adult. Practically speaking, this means my younger boy moves about twice as fast as me.
One may wish to assert that the above equation is obviously false because infants, as we all know, can’t move very fast. While they may initially appear to be an exception, it is useful to note that they make an awful lot of jerky, uncontrolled movements which would probably average to the correct mean velocity.
I have, on occasion, considered taking measurements to validate the theory, but I just haven’t had enough energy.
I also blog at Engineer Blogs, home away from home to some of the best engineering blogs.
Comments»
No comments yet — be the first.