FCIWYPSC

Teaching math without memorization March 2, 2011

Posted by mareserinitatis in education, gifted, homeschooling, math, older son, teaching.
Tags: abacus, arithmetic, bead frame, gifted education, homeschooling, math, multiplication, tables
12 comments

If there is one thing I learned in my junior level electromagnetics class that will always stick with me, it’s this:

The permittivity of free space (ε) is 8.854 * 10 ^-12 F/m.

And realizing that will always stick with me gave me a lot of insight into what is wrong with the typical approach to teaching math, especially in elementary school.

I know it’s a stretch, but bear with me.

(Totally gratuitous picture of a cute baby bear.)

One of the things I’ve encountered with both my kids is that their teachers are very set on them memorizing math facts. My older boy spent 3rd and 6th grade enrolled full-time in regular public school programs, and his third grade teacher was constantly railing on about how he was ‘bad in math’. In fact, she blamed it on the fact that he’d been homeschooling. (We got this every time we talked to her.) She would go on and on about how he didn’t have his tables memorized. Why, he had to stop and think every time she asked him a basic addition problem!

OMG…thinking in school?! Can’t have that.

I therefore found it very amusing when, prior to the the next school year, his principle pulled out the results of his spring MAPS testing and commented on how good his math scores were because, in her words, “He must know his tables really well.”

By these two comments alone, you can tell what is important to elementary school teachers: memorization of arithmetic tables.

Aside from having a BS in physics, I minored in math in college. Despite the fact that I had enough credits for a major, the credits were in overwhelmingly applied math classes, and there was no applied math major at my school. Suffice it to say that I do have at least a basic knowledge of math.

I also have homeschooled my older child for most of his educational career, and as a freshman in high school, he’s finishing a course in college algebra and trigonometry.

During the older child’s homeschooling years, I never once made an attempt to have him memorize tables of any kind. I did not practice a lot of repetition of basic facts, either. This was because of my experience in my electromagnetics class: I didn’t memorize the value of the permittivity of free space due to repetition and drill; I memorized it because I used it in nearly every problem I did for four months in that class. Yeah, I had to look it up the first dozen times I used it, but after that, it was lodged in my brain. And look…it’s still there a decade later!

I came to the conclusion that if you really need to know something, you’ll learn it through frequent use. But how do you use something that you don’t know?

Addition and subtraction are fairly simple: you give a kid a bead frame, abacus, or even a ruler (the original slide rule!) and show them how to perform addition and subtraction operations using beads or moving up and down a number line. Then you can move them quite quickly through addition and subtraction of infinitely (okay…not infinite) finitely large numbers.  You can let them go through increasingly complex topics without ever making them memorize a table.  In fact, after a short time, you’ll find that they are pointing at beads or rulers in the air, counting out the solution to their problem.  And after that, the invisible ruler or beads will be sitting in their head, being manipulated by mental fingers.  Finally, they won’t even have to think about it…they’ll just know.

The image on the left is an abacus, while the image on the right is a bead frame. Bead frames are easier to find and manipulate, in my experience.

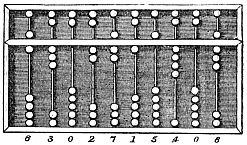Multiplication should be taught as addition of groups of objects, and division as ‘counting’ of the number of groups in the whole. Once kids have mastered the process of multiplication and division, you can then simply print out a multiplication table. I had my older son paste it on the inside cover of a notebook or the front of a folder so that he could always find it. You may find that some kids prefer to go back to the bead frames.  (And if you are really lucky, you have an abacus and know how to use it for multiplication…which I don’t.)  Any method is fine as long as it works for your child. But the point is that you can then let them progress through more and more complicated arithmetic involving those operations (such as multiplying large numbers or long division) using the table or other device to look up values. Again, as you progress through these concepts, they will slowly begin to memorize them.

As a homeschooler, the curriculum that I chose for math was fairly important as well. I liked Singapore math for it’s focus on simplicity and conceptual explanations. Everyone raves about the ‘mental math’ tricks that are taught in the series. And they’re right: mental math is awesome. However, the only reason the series does it so effectively is because it teaches the concepts in a way that you can then make logical simplifications in process that result in ‘mental math’ and good estimation skills.

(My only complaint is that they don’t teach the lattice method of multiplication. I think the ‘traditional’ method of multiplying large numbers is much better suited for estimation methods, whereas the lattice method is definitely superior for calculating with precision.)

To me, the important part of all of this is to make sure that they understand what the process of addition, subtraction, multiplication, and division. Kids can memorize facts for quick recall, but if that is the emphasis and they can’t recall a fact, they’re going to be stuck.  If the emphasis is instead on teaching arithmetic as a process, they can always figure it out should they forget.

And really, arithmetic is a process.  I came across an article on Hoagies’ Gifted site called Why Memorize? I have to take big exception to the article because it says that math is a lot of dry facts.  If you teach it as memorization of facts instead of a process of manipulating numbers (or objects or motion in space), it sure is!  But I can tell you that it’s not, and as you advance to higher level classes in mathematics, reliance on the notion that math is memorization will cause you problems and impede your progression.

Finally, I have to wonder if this is why so many elementary school educators fear math: it’s boring memorization of facts.  They are never taught how it’s actually a really cool process.  If it were taught properly, preferably with a lot of enthusiasm instead of dread, I wonder if a lot of teachers would lose their ‘math-phobia’.   And that would, of course, mean their students might start to like math, too.