FCIWYPSC

Repost: Planet of Youth March 27, 2011

Posted by mareserinitatis in education, math, physics, science, teaching.
Tags: acceleration, age, gravitation, physics, planets, velocity
trackback

If you’ve ever wondered how old you are in Jupiter years, this is your chance to find out. All you need are the following: your age in earth days, the mass of sun and the distance between the planets and sun. And Math!

Note: The reason you are using variables for most of the project is so that you can use any planet you want. If you did this for each planet using numbers, you would have to do everything over for each planet. If you want to cheat and avoid the math (as well as get a more exact value), you can check out Your Age on Other Planets.

These are the variables we will be using:

G is called the gravitational constant (we’ll give you this later)
M_s is the mass of sun
M_p is the mass of the planet
A is the acceleration (how much it’s speed changes in time)
R is the distance of the planet from the sun

First use the following equations:
(1)

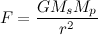
This is Newton’s Law of Gravitation.

This says that the force exerted on a planet is proportional to the mass of the planet, M_p, and the mass of the sun, M_s. It is inversely proportion to the distance between the planet and the sun, squared, or R². If you increase the mass of the planet or the mass of the sun, the force will increase. On the other hand, the force will decrease if you increase the distance between the two. However, the decrease isn’t linear – that is, it doesn’t decrease a fixed amount for a change in distance. It will change based on the square of the distance, faster than if the distance wasn’t squared.

(2)

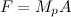
This is Newton’s Second Law

This equation states that the force on the planet is equal to its mass times its acceleration.

Both equation (1) and equation (2) are equal to the force. Set them as equal to each other (using the transitive property: if a=b and b=c, then a=c). Then solve for A.

Your result should show that the acceleration on the planet only depends on the mass of the sun and the distance between the planet and the sun. The acceleration isn’t affected by the mass of the planet!

Now we’ll give you another equation for A:

(3)

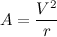
The is the acceleration of a circular path (the orbits of the planets are very nearly circular)

What this equation says is that the speed changes by a factor of the speed (V) squared over the distance between sun and the planet. If you ever want to get into Newtonian mechanics, you’ll run into this as a basic result for how speed and acceleration are related when an object moves in a circular path.

2. Use your two equations for A (the one above and your result from Exercise 1) and solve for V, your velocity (or speed).

3. Now that you have an equation for the velocity, you know how fast the planet is moving. Again, the speed of the planet has nothing to do with the planet’s mass: it is only affected by its distance from the sun. The farther from the sun that the planet is, the slower its speed.

Let’s figure out how far the planet has to travel to make one orbit around sun. If the path traveled is a circle, and the radius is R, what is the circumference of the circle? Set this formula equal to distance, D.

4. We know how far the planet has to travel around the sun and how fast it goes. Let’s figure out how long a year is on that planet. Since speed is distance over time (V=D/T), we can rewrite this. Solve for T.

5. Now substitute your equations for V and D into your formula for T. This will give you an equation for the length of the year.

6. Now let’s test our answer. First, figure how long is an earth year in seconds? (Hint: the number of days in an earth year is 365.25.) Your answer (and all future answers) should have four significant digits. The answer will be your Converted Answer.

7. Use your formula for T to figure out how many seconds are in an earth year. The value for π is 3.14159, G is 6.67•10^-11 N•m²/kg², the mass of the sun is 1.99•10³⁰ kg, and the radius of the earth’s orbit is 1.50•10¹¹ m. Your answer will be in seconds. This is your Calculated Answer.

8. Now figure out how accurate your calculation is. The formula to calculate percent error is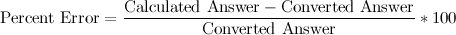

Your Percent Error should be less than 1%. If it is not, try to look for an error in your calculations.

9. Now use your formula to calculate the number of seconds in a year for your planet. Planetary radii are listed below.

Planet:______________________ Radius: _______________________________

Conversion Factor: __________________

10. How old are you in seconds? Multiply the number of seconds in an earth year, your Calculated Answer, by your age in years.

11. Now divide your age in seconds by the length of a year on your planet. How many years old are you on that planet?

12. Check your answer. You have been given a conversion factor for your planet. Divide your age by this number.

13. Now check how close your answers were. If your answer to 11 is your calculated answer, and your answer to 12 is your converted answer, use the equation in 8 to find your percent error.

Now ask someone older than you how old he or she is on Mercury.

——

This chart is for the instructor. Once the student has completed Exercises 1-8, they can get the information for their particular planet(s). The conversion factor is actually the number of earth years it take for that planet to make one revolution around the sun.

Planet	Radius (m)	Conversion Factor
Mercury	57.9•109	0.241
Venus	108•109	0.615
Mars	228•109	1.88
Jupiter	778•109	11.9
Saturn	1430•109	29.5
Uranus	2870•109	84.0
Neptune	4500•109	165
Pluto	5900•109	248

In case someone wants them, these are the answers to exercises 1-8.

1.

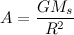
2.

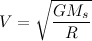
3. D=2πR

4. T=D/V

5.

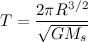
6. 31 557 600 seconds/year

7. 31 680 000 seconds/year

8. 0.39%