Never ask a woman her weight…but her kinetic energy is fine August 2, 2014
Posted by mareserinitatis in math, physics, running, science.Tags: blerch, gravitation, kinetic energy, mass, physics, runners, running, science, velocity
add a comment
Today, I had one of the most awesome runs I’ve ever had. In particular, I sustained a much faster pace than I have over a 3 mile distance.
I couldn’t help but wonder, however, about the factor weight plays in one’s speed. As much as I try not to worry about weight and focus on being healthy, there’s this part of me that thinks it would be cool to lose a bit of weight because then I would go SO MUCH FASTER. Or at least that’s what I tell myself. However, I wondered if maybe I was exaggerating a bit, so I decided to check it out.
While it’s a bit of an oversimplification (that doesn’t take into account muscle tone, lung capacity, hydration, electrolyte levels, altitude adjustment, and the 18 bazillion other things that can affect a runner, even as stupid as that kink that’s still in your neck from last Thursday’s swim (okay, that only affects the triathletes here)), a quick check is to use the kinetic energy equation.
First, of course, we have to assume a perfectly spherical runner. Or a Blerch:
(As an aside, if you don’t know what the Blerch is, you must check out the Oatmeal’s wonderful cartoon on running. We all have a Blerch deep inside of us.) Either way, perfectly spherical things are happy for physicists because of all the lovely simplifications we can use in learning about them. So, if you’re a perfectly spherical runner, remember that physicists will love you.
Anyway, our hypothetical runner will have a mass (m), which is, of course, directly proportional to weight. (Weight, of course, is also referred to as gravitational attraction, so the more you have of it, the more attractive you are, at least from the perspective of the planetary body you’re closest to. Also, it may start to be more attracted to you if your velocity starts to approach the speed of light. Maybe this is why many humans also find runners attractive? Not sure.) The unit of mass is the kilogram. The runner will also have to maintain an average speed velocity (v), and of course your pace is inversely proportional to your velocity. Your velocity is probably measured in miles per hour by your local race, but since we’re being scientific, we could also use SI units of meters/second. That being said, if you double your speed in one unit, it will also double in the other. There’s nothing fancy that happens because you’re using one unit or the other.
The kinetic energy of our runner, assuming an average velocity, can be written as
(1) KE=½ mv2
If we have the kinetic energy and mass, but want to find out the velocity, we first divide both sides of the equation by the mass and then take the square root of both sides. This leaves us with the following result:
(2) v=√(2 KE/m)
Let’s take an example. If we have a runner who has a velocity of 5 mph (or 2.2352 m/s) and a weight of 140 lbs. (or 63.5 kg). If we use SI units to compute this runner’s velocity, it turns out her initial kinetic energy (KEi) is 158.63 J.
On the other hand, we don’t really need to know how much initial kinetic energy the runner has, in terms of numbers. We can just define it as the quantity KEi. It turns out that physicists are kind of lazy about using numbers, so we’ll try to go without them because, in my opinion, it sort of confuses things. (You’ll see why later.)
How this this help us? Well, if you want to take a drastic example, let’s assume a runner loses half of her body weight.
First, let’s establish that her initial kinetic energy is defined also by an initial mass mi and velocity vi. (These would be the same as the 5 mph and 140 lbs. above.) This means her initial kinetic energy can be written as
(3) KEi=½ mivi2
and her initial velocity would therefore be
(4) vi=√(2 KEi/mi).
If her weight drops by half, we can write this as her initial weight divided by 2:
(5) m=mi/2
If we put (5) into our velocity equation (2) as our new mass and keep the same initial kinetic energy, we get
(6) vnew=√(2 KEi/m)=√(2 KEi/(mi/2))=√2*(2 KEi/(mi))=√2√(2 KEi/(mi))
You can see that the last part in six is basically the square root of two times our initial velocity from (3). That means that by losing half her weight, our runner would run about 1.4 times as fast, or 40% faster.
Now what if she only loses 10% of her weight? It turns out that (5) would become
(7) m=mi/1.1
so our new velocity would be the initial velocity times the square root of 1.1, which is about 1.05. Losing 10% of her weight only makes her 5% faster.
After spending time looking at this, I decided that going on a massive diet definitely isn’t going to help me speed up significantly. (In fact, if I manage to go from my current weight to my ideal, I would maybe get a gain of a bit over 1/2 mph.) It’s the fact that the mass doesn’t play as strong a role as velocity does because velocity gets squared and mass doesn’t. If you want to go faster, you are better off practicing running faster.
So please pass the ice cream! I need it for my fartlek recovery.
To run or to run/walk…that is the question December 2, 2012
Posted by mareserinitatis in math, physics, running.Tags: distance, integrals, jingle bell run, running, speed, velocity
add a comment
Yesterday was the Jingle Bell Run. It’s a 5k that doubles as a fundraiser for the Arthritis Foundation. My team did fairly well for fundraising, coming in 6th place overall. This is rather impressive because our team had 3 people, and all the groups ahead of us had at least ten. If they had averaged it out per person, we definitely had the highest donations per teammate. One of my teammates was the second highest fundraiser overall…and got a certificate for an hour massage.
We got to wear elf costumage while running. How cool is that? (And no, Gigadog didn’t run. I attempted to a couple times, but after almost faceplanting when the leash got tangled around my legs, I didn’t feel like I could keep training with her.)
Actually, we were worried that we were going to be overdressed, but it turned out that people go all out for the race. There were elves galore and many wearing santa hats. There were also people dressed in costumes – angels, reindeer, christmas trees, and even full-blown nativity scenes complete with puppy dogs dressed in lamb’s clothing. (The owners were dressed as shepherds.)
All in all, a good time.
An interesting conversation occurred later, however, when we talked about running versus running/walking. Last year, when I started running, my goal was to run a 10k straight through. I managed to do that, but I noticed my progress was rather slow. This year, I’ve started using a program where I do running and walking intervals, and I’m noticing a huge difference: my rate of improvement has really increased from month to month. The topic came up with a friend’s husband, who said it just makes more sense to run straight through. He had a hard time believing me when I said I could actually go faster with walking breaks.
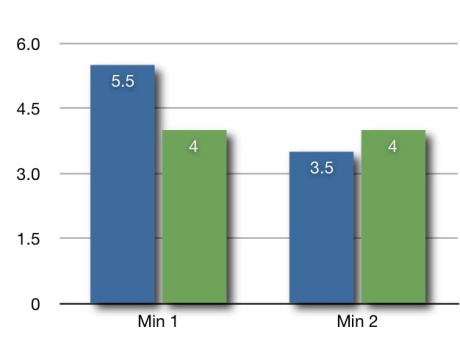
An easy way to see this is with a graph:
Unfortunately, my legend got scrubbed, but what we have are actual speeds from different exercise sessions I’ve done. (Yes, I know I’m slow…but I needed data.) The blue comes from near the end of the race yesterday, while the green is from a timing run I did (no walking) a couple weeks ago.
If you’ve taken basic physics, you know that the integral of the velocity over time gives you the distance. For those who don’t know calculus (or integrals), and easy way to see this is to look at the area of the bars. You can see that the area of the two blue bars together is greater than the area of the two green bars together.
Another way we can think about it is to calculate distance over an hour. The speed shown by the green bars is 4 mph. In one hour, assuming I can maintain this pace, I will travel 4 miles in that hour. However, if I run half an hour at 5.5 mph and walk the other half at 3.5 mph, those distances will be 2.75 miles and 1.75 miles and will sum to 4.5 miles. While this isn’t a lot faster, it’s a noticeable difference.
Apparently running faster for half the time does more to improve my speed than running the same time interval with a slower pace.
I’m sure hoping so, anyway. I signed up to do a half marathon next spring, and I’ve gone from hoping I can finish in less than four hours to wondering if I’ll be able to make it in three. Keep your fingers crossed for me.
Repost: Planet of Youth March 27, 2011
Posted by mareserinitatis in education, math, physics, science, teaching.Tags: acceleration, age, gravitation, physics, planets, velocity
2 comments
If you’ve ever wondered how old you are in Jupiter years, this is your chance to find out. All you need are the following: your age in earth days, the mass of sun and the distance between the planets and sun. And Math!
Note: The reason you are using variables for most of the project is so that you can use any planet you want. If you did this for each planet using numbers, you would have to do everything over for each planet. If you want to cheat and avoid the math (as well as get a more exact value), you can check out Your Age on Other Planets.
These are the variables we will be using:
G is called the gravitational constant (we’ll give you this later)
Ms is the mass of sun
Mp is the mass of the planet
A is the acceleration (how much it’s speed changes in time)
R is the distance of the planet from the sun
First use the following equations:
(1) 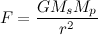
This is Newton’s Law of Gravitation.
This says that the force exerted on a planet is proportional to the mass of the planet, Mp, and the mass of the sun, Ms. It is inversely proportion to the distance between the planet and the sun, squared, or R2. If you increase the mass of the planet or the mass of the sun, the force will increase. On the other hand, the force will decrease if you increase the distance between the two. However, the decrease isn’t linear – that is, it doesn’t decrease a fixed amount for a change in distance. It will change based on the square of the distance, faster than if the distance wasn’t squared.
(2) 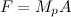
This is Newton’s Second Law
This equation states that the force on the planet is equal to its mass times its acceleration.
Both equation (1) and equation (2) are equal to the force. Set them as equal to each other (using the transitive property: if a=b and b=c, then a=c). Then solve for A.
Your result should show that the acceleration on the planet only depends on the mass of the sun and the distance between the planet and the sun. The acceleration isn’t affected by the mass of the planet!
Now we’ll give you another equation for A:
(3) 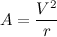
The is the acceleration of a circular path (the orbits of the planets are very nearly circular)
What this equation says is that the speed changes by a factor of the speed (V) squared over the distance between sun and the planet. If you ever want to get into Newtonian mechanics, you’ll run into this as a basic result for how speed and acceleration are related when an object moves in a circular path.
2. Use your two equations for A (the one above and your result from Exercise 1) and solve for V, your velocity (or speed).
3. Now that you have an equation for the velocity, you know how fast the planet is moving. Again, the speed of the planet has nothing to do with the planet’s mass: it is only affected by its distance from the sun. The farther from the sun that the planet is, the slower its speed.
Let’s figure out how far the planet has to travel to make one orbit around sun. If the path traveled is a circle, and the radius is R, what is the circumference of the circle? Set this formula equal to distance, D.
4. We know how far the planet has to travel around the sun and how fast it goes. Let’s figure out how long a year is on that planet. Since speed is distance over time (V=D/T), we can rewrite this. Solve for T.
5. Now substitute your equations for V and D into your formula for T. This will give you an equation for the length of the year.
6. Now let’s test our answer. First, figure how long is an earth year in seconds? (Hint: the number of days in an earth year is 365.25.) Your answer (and all future answers) should have four significant digits. The answer will be your Converted Answer.
7. Use your formula for T to figure out how many seconds are in an earth year. The value for π is 3.14159, G is 6.67•10-11 N•m2/kg2, the mass of the sun is 1.99•1030 kg, and the radius of the earth’s orbit is 1.50•1011 m. Your answer will be in seconds. This is your Calculated Answer.
8. Now figure out how accurate your calculation is. The formula to calculate percent error is 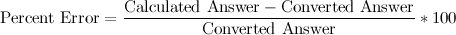
Your Percent Error should be less than 1%. If it is not, try to look for an error in your calculations.
9. Now use your formula to calculate the number of seconds in a year for your planet. Planetary radii are listed below.
Planet:______________________ Radius: _______________________________
Conversion Factor: __________________
10. How old are you in seconds? Multiply the number of seconds in an earth year, your Calculated Answer, by your age in years.
11. Now divide your age in seconds by the length of a year on your planet. How many years old are you on that planet?
12. Check your answer. You have been given a conversion factor for your planet. Divide your age by this number.
13. Now check how close your answers were. If your answer to 11 is your calculated answer, and your answer to 12 is your converted answer, use the equation in 8 to find your percent error.
Now ask someone older than you how old he or she is on Mercury.
——
This chart is for the instructor. Once the student has completed Exercises 1-8, they can get the information for their particular planet(s). The conversion factor is actually the number of earth years it take for that planet to make one revolution around the sun.
| Planet | Radius (m) | Conversion Factor |
| Mercury | 57.9•109 | 0.241 |
| Venus | 108•109 | 0.615 |
| Mars | 228•109 | 1.88 |
| Jupiter | 778•109 | 11.9 |
| Saturn | 1430•109 | 29.5 |
| Uranus | 2870•109 | 84.0 |
| Neptune | 4500•109 | 165 |
| Pluto | 5900•109 | 248 |
In case someone wants them, these are the answers to exercises 1-8.
1. 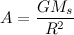
2. 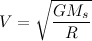
3. D=2πR
4. T=D/V
5. 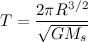
6. 31 557 600 seconds/year
7. 31 680 000 seconds/year
8. 0.39%


 I also blog at Engineer Blogs, home away from home to some of the best engineering blogs.
I also blog at Engineer Blogs, home away from home to some of the best engineering blogs.