FCIWYPSC

Getting hot under the sheets August 1, 2010

Posted by mareserinitatis in electromagnetics, engineering, physics, science.
Tags: bed, cancer, electromagnetics
10 comments

A couple days ago, I wrote about a post which was a knee-jerk reaction to an article I’d read on Sci-Am. The actual paper is “Sleep on the right side—Get cancer on the left?” by Örjan Hallberg and Olle Johansson, published June, 2010 in the journal Pathophysiology.

Now that I’ve had the time to sit down and read it, I’m no less boggled. There are several problems with the paper.

As far as the paper itself, it does absolutely nothing in the way of taking measurements or providing simulation data. The data upon which they are basing their argument is this: there have been studies showing that there is a higher incidence of certain cancers on the left side of the body than the right. Also, people have a preference for sleeping on the right side of the body. Therefore, the two are connected together by beds and they state a proposed relationship between beds and cancer with absolutely no supporting evidence aside from those studies. In other words, they have correlation between cancer and preference for sleeping on the right side. That is the entirety of the empirical data.

First, the authors state that preference for sleeping on the right side doesn’t necessarily imply that people spend more time sleeping on their right side. Second, there are also anti-correlative relationships between other types of cancers and disorders and side-sleeping. Right there I would be scratching my head and wondering about the validity of any correlation.

I mean, here we have another correlation:

Okay…maybe they’re anti-correlated.

However, I’d like to focus on two excerpts from the paper in particular. The introductory paragraph states:

There is no doubt that horizontally polarised radiation
emitted from western-type FM broadcasting towers may
interfere with a human body at night during sleep. This is
a logical consequence of wavelengths normally used for FM
and TV broadcasting. A metal-containing mattress may act
as a half-wave antenna, thus the central parts of the body may
become more exposed to resonant currents than the head and
feet are.

In the results and discussion section, they state:

Basic physics tells us that a structure that is approximately
1.5 m long may become resonant (half-wave resonance) at
frequencies of approximately 100 MHz, since half a wave-
length is 1.5 m. Half-wave resonance reaches a maximum
in the middle of the structure. If this structure is resting on
(above) a metal bed and is exposed to horizontally polarised
waves, the incident wave and a reflected wave will produce
a standing wave pattern. The field strength will be almost
zero close to the surface of the metal base, but reach a max-
imum a quarter wavelength (75 cm) above the metal base,
another zero at 1.5 m above the metal base and so on. The
field strength at the maximum is twice the field strength if
the bed was not there, due to summation of the incident and
reflected waves. Without such a metal base there will be no
standing waves driving currents along and inside the body.

I am bothered because there are absolutely no references for any of the above assertions. How does it interfere? What’s the mechanism? Where is the data confirming this?

When looking at the electromagnetics, I am seeing the author set up two different scenarios, and I don’t think they realize they are doing so. The first excerpt states that the metal bed frame is behaving like a quarter-wave antenna with a current distribution strongest in the middle of the bed (near the torso) and weakest near the head and feet.

In the second excerpt, they’re saying that you have a resonator (a human being) above a ground plane, which is reflecting. Let’s look at both scenarios, beginning with the second.

Let’s think about the bed like a hunk of metal floating in space and, for a moment, ignore the person lying on top of it. I made the mistake before of thinking about the mesh and springs separately. Really, they’re all so interconnected and the spaces between them is small relative to the wavelength, we can treat it like a large piece of metal. So really, it’s a scatterer/reflector or possibly a ground plane. Either one will reflect a field that impinges on it.

We’re going to assume plane wave reflection. The angle of incidence will be the same as the angle of reflection.

If you look at the graphic above (which I borrowed from the hyperphysics website…you should go visit there), you can see that there is an interference pattern between the incident and reflected waves. The places where the blue lines cross or you can see the background will be constructive interference (the crests or troughs will add, making a larger wave) versus the place where a blue line and tan cross, where we have destructive interference. The authors claim that constructive interference is a problem in this scenario.

We can actually use simple geometry to determine where the constructive interference will occur. It turns out that the formula is d = λ/(4 sin θ_i) where d is the distance above the plane, λ is the wavelength, and θ_i is the incident angle.

The authors of the paper state that this interference will be at a maximum (i.e. the wavefronts will be in phase or produce constructive interference) at 75 cm above the bed. However, that’s only true if the angle of incidence is 90°. That means the radio waves would have to be coming straight down onto the bed. Not likely.

Let’s assume that a 100 m tall radio tower is about 4 miles away (or about 6500 meters), the actual angle, neglecting curvature of the Earth (which we frequently do in Fargo), is closer to 0.88°. The maximum in that case will occur at 1200 m above the bed. Unless you live in a fairly tall building (like skyscraper tall), I think that’s well out of the range of your bedroom.

If we give the authors a bit and assume that maybe the transmitter is on a hill someplace, an angle of 10° says the maximum will occur about 5.75 m above the bed…probably in the apartment two stories above you. (I hope you feel guilty for affecting your neighbors upstairs this way.)

Keep in mind, however, that we do not have an infinite ground plane; it is only about a wavelength long. Constructive interference only happens above the bed at angles within 45° relative to the normal of the bed. A low angles, like I’ve examined here, the constructive interference will actually happen somewhere away from the bed because it has to occur past the point where the wave is reflected. Therefore, a higher incidence of cancer in the torso versus the head and feet would actually imply that constructive interference probably does not play a role.

Now that we’ve ruled out constructive interference from reflection, let’s look at the possibility that the bed is behaving like an antenna. It can’t be because it’s isolated from any sort of path that would remove energy. But let’s ignore that (significant) detail for a moment.

Now it may be true that an antenna may be receiving power and, in this process, re-radiate some of the power. Let’s make the assumption that the bed is, in fact, acting like an antenna that is absorbing everything that it receives and then re-radiating everything. (This is also slightly unrealistic because, if the body is absorbing the wave, the wave cannot also be passing through to the bed, which will re-radiate it. Let’s not let reality stop us from believing this, though.) We need to compute how much power a person would actually be receiving from an antenna.

All we need is the Friis transmission equation.

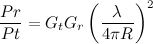
Assuming an antenna 4 miles away, transmitting at a frequency of 100 MHz (giving a wavelength of 3 meters, as the authors assumed), a max EIRP of 100 kW (this is the product of the transmitter gain and power), and a perfectly absorbing human with a gain of 1, a person would receive approximately 136 uW (microwatts) over your entire body. This is equivalent to 136 uJ per second. However, we are going to assume that it’s twice that because we have both the initial wave as well as the wave radiated by the bed springs.

The most plausible mechanism for cell damage by electromagnetic non-ionizing radiation is by heating, so let’s figure out how much this energy will heat you up. Of course, this assumes that all of the electromagnetic energy will be converted to thermal energy, which is highly unlikely. Given our bodies are mostly water, and the lowest resonant frequency of water is 2.5 GHz (which is the operating point for most household microwave ovens), I’m not exactly sure any of this would be converted to thermal energy. Remember that it takes 4.184 Joules to heat one gram of water by 1°C. This is the specific heat of water or c. The average mass (m) of a US citizen is about 80 kg. Using the specific heat equation,

,

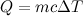this means that our body will heat up 8*10^-10°C per second or 48*10^-9°C per minute. By contrast, standing out in the sun gives you 1.96 calories or about 8 Joules per minute, changing your body temp by 2.4*10^-5°C per minute. This is, at least, three orders of magnitude larger.

Sometimes it gets a little hot under the sheets, but I don’t think it’s due to radiation from TV and radio antennae.

In any case, the bed hypothesis doesn’t make sense because there is no way for it to work. If the bed is behaving like a reflector, the constructive interference is so far away for a realistic case as to make it absurd to propose a relationship. In both the case of a reflector or antenna, there is so little power that it couldn’t do anything. Therefore, I am certain that, if there is a relationship between side-sleeping and laterality of cancer, electromagnetics plays no role.