Students finding their direction June 23, 2012
Posted by mareserinitatis in education, engineering, geology, geophysics, physics, research, teaching.Tags: engineering, geophysics, majors, math, physics, students
add a comment
The younger son’s birthday was this week, and we opted to host a pool party at a local hotel. (IMO, pool parties are the best for the elementary school age group: they keep themselves busy and then go home exhausted.) I was checking in when I noticed a young man standing at the other end of the counter. He looked familiar, so I asked if I knew him.
“I took your class last fall.”
“Oh great! How did the rest of the school year go for you?”
“Great. I actually switched to business and am really liking it.”
“Really? Why did you switch?”
“I just figured I liked business a lot better.”
“That’s why they have you take those early major classes – so that you find out you don’t like it before you get too far into it.”
I think the poor kid thought I would be mad that he had switched. But I wasn’t mad at all. If he feels like he’d be better off in a different major, then he ought to go for it. And that is part of what I’m trying to set out in the class – this is what engineers do. If it doesn’t look fun, then you ought to think about a different major. That’s a perfectly valid choice, and no one should judge a student for it.
(Yeah, I know…I sit here and wring my hands because older son gets these obnoxiously high scores in math and science but wants to be a writer…I’m one to talk.)
But seriously, I actually think it’s sort of silly to make students choose a major really early on in school. I think it’s a good idea to try to take a lot of classes in different fields before you really choose. I say this as someone who major hopped a lot during undergrad. I spent some time in physics, chemistry, journalism, and graphic arts. I finally decided that I liked physics after all, but what got me excited was geophysics. I happened to take a geology class when I was at Caltech because I had to take a lab course, and everyone told me geology was the easiest. Turns out, I really liked it and did very well in the course. (Of course, later on, I found that geology feels too qualitative and prefer geophysics, so it all worked out. On the other hand, I think I would’ve liked geology better if it had all been field courses.) :-)
I have run into people who got upset with me for this type of thing. I was doing research with a professor in undergrad, but I felt like the research wasn’t going well and got sort of excited about a math project that I’d seen a professor give a talk about. I talked to that professor to see if he’d be interested in having me as a student, which he was. When I told the other professor that I was going to work with the math professor, all hell broke loose. (I still think I made the right choice, though, especially since the first project really never did go anywhere.) I have yet to figure out why the first professor got upset, though, and did some petty stuff, like kicking me out of the student office (despite no one needing a spot) and having the secretary take away my mailbox. (This was silly, BTW, as I was president of the Society of Physics Students, so she ended up giving it back to me a month later so I could get SPS mail.)
And what did this do? Certainly reinforced that I didn’t want to work with this person, but I could also see it making a student feel like this person is representative of a particular field. Wouldn’t you wonder if a student would not want to go into a major because of the way the professors treat him or her? I can (and did!), and it just shows how ridiculous the whole thing was.
No, students need some time to explore their interests and getting mad at them for not doing what you think they should do is silly. They are the ones who have to deal with the consequences of their choices, and if a student takes my class and decides they don’t want to spend the next five to ten years of their life studying engineering, then I think they’ve learned something very important and just as valid as anything else I have to teach them.
When I was at the conference… March 13, 2012
Posted by mareserinitatis in electromagnetics, engineering, physics, research.Tags: conference, engineering, physics, research
add a comment
When I was at the conference last week, I had one fellow come up and look at my poster. He is working on a similar problem but in a different application, and he made some comment about how he definitely thought what I was doing had merit. (After seeing his talk, it made sense because he was trying something similar.)
However, we spent about 20 minutes arguing as to what we thought was going on in one of my plots. He kept suggesting something that I had ruled out with experiment.
Tonight I’m looking at papers on some theory related to this project, and I think I have managed to find the answer to that mysterious plot. Sadly, I was way off in my explanation, but I have to admit that apparently I wasn’t the only one. The fellow I was arguing with had it wrong as well.
The real answer appears to be way cooler than either of us thought. I love physics.
Pinewood derby: What a drag! January 16, 2012
Posted by mareserinitatis in engineering, physics, science, younger son.Tags: air resistance, cub scouts, drag, energy, energy conversion, friction, gravitational energy, physics, pinewood derby
4 comments
My husband son competed yesterday in my son’s his scouting group’s pinewood derby race. For those of you who have never had a kid in cub/boy scouts, they hand out these blocks of wood that you get to make into a car. The idea isn’t to win the race: it’s supposed to be that dads and their boys spend some time bonding over manly things like woodworking.
(One year, Mike was out of town during this whole thing, so I got to be manly and help the older boy build his car. All I can say is that Dremel tools are awesome.)
If you look on the web, you’ll find a lot of advice on how to prep pinewood derby cars and make them faster. One thing that consistently bugs me is that one should pay attention to aerodynamics of the car and give it a low profile.
This makes me nuts.
To understand the following, you might want to know what a track looks like. So here you go:
Let’s start out with the specifications. Most pinewood derby tracks have a height of about 4 feet and a length of 32 feet. I also will note that the ones we’ve raced on were wood, not aluminum.
Most of the pinewood derby cars I watched made it the whole 32 feet, though not all did. So let’s say that, on average, they travel 32 feet. The *fastest* ones traveled at an average speed of 10 ft/s (or 3 m/s). The maximum they can weight 5 oz. or 140 g.
What we’re going to do here is look at how much energy the system puts into overcoming air resistance versus friction. It’s very hard to figure out exactly how much goes into friction simply using equations, so we’re going to figure out the total energy and the energy lost to drag forces. Once we have those two quantities, we can subtract the drag forces from the total energy and assume that the difference is equal to the frictional losses. Finally, we can compare the drag and frictional losses.
First things first: what is our total energy? It starts out entirely as potential energy as the cars are placed at rest on the top of the ramp. Potential energy is, fortunately, very easy to calculate. It is simply the product of the height of the object, its mass, and the gravitational acceleration. In other words,
![]()
We know the mass of the car (0.14 kg), the height is approximately 1.22 m, and the graviational acceleration is 9.8 m/s2. This results in a total potential energy of approximately 1.67 J.
The potential energy is equal to the total energy in the system since the cars start with no other kind of energy. In a frictionless and drag-free system, all of this energy would be converted to kinetic energy and the cars would drive forever at the same speed once they reached the bottom of the ramp. Obviously, however, that’s not what happens. Eventually, all of the energy is converted to friction and drag, and the cars stop.
Now we need to determine the drag on the cars. The drag equation is:
![]()
The drag force is proportional, therefore, to the density of the fluid (ρ), velocity (v), drag coefficient (CD), and cross-sectional area (A).
The density of the fluid (air) is approximately 1.2754 kg/m3, and the velocity is 3 m/s. The cross-sectional area of the car, at maximum, is 2.75 x 3 in. In real *ahem* units, this is 0.00532257 m2.
The drag coefficient for a long cylinder, according to Wikipedia, is 0.82. Given the cars are all sorts of different shapes, I think this would probably be the closest approximation, although for some cars, this will be high.
All of this put together gives us a force of 0.025 N. Over a distance of 32 feet (or 9.75 m), this gives an energy of 0.24 J.
If we assume that all of the potential energy is converted to either drag or friction, that means 0.24 J is converted to drag while 1.43 J goes into friction. This means that roughly 14% of your energy losses are due to drag while the other 86% are due to friction.
My advice, therefore, is to not worry so much about drag and the aerodynamics of the car and to worry far more about the ways to reduce friction.
What should you do to help your pinewood derby car to be fast? There are three things:
1) You want to maximize your potential energy, so being as close to the 140 gram maximum weight is good. You can get all sorts of weights commercially to assist with this. Some people have argued that putting the weights near the back of the vehicle helps even more. I wouldn’t doubt this as you’re putting the weight at greater height, giving the car more initial energy to start with.
2) The biggest issue is reducing the friction between the wheel and the axle, and there are a few easy ways to do that: sanding and polishing the axles as well as using graphite or teflon as a lubricant. (Our troupe doesn’t allow graphite because it marks the floors, but teflon is allowed.)
3) Reduce the friction between the car and track. The best way to do this is to make sure your wheel alignment is as straight as possible as this will keep it from rubbing against the center of the track.
The winner of our pinewood derby actually had a very blocky car designed to look like a platypus. I’m guessing the winner didn’t spend much time focusing on aerodynamics and instead chose to minimize their frictional losses.
It went boom November 27, 2011
Posted by mareserinitatis in education, physics, science, teaching.Tags: bombs, explosions, flaming tube, physics, rubens tube
1 comment so far
A few years ago, I was working on as part of an NSF educational program. The idea was to pair students (undergrad and grad) with local science and math teachers to help them do whatever they needed. I was paired with a physics teacher who asked me to build a Ruben’s tube. (I suppose I should put the instructions here some day…they’re still on my old blog.)
If you’re not sure what I’m talking about, here’s a video of the demonstration. I’m holding the speaker at the end of the metal tube that’s covered with saran wrap. The noise from the speaker is vibrating the saran wrap and hence the gas inside the tube. At the right frequencies, you get standing waves, which is visible in the flames coming from the top of the tube:
Anyway, as a safety measure, we started by throwing some dry ice in the tube. This was supposed to evacuate out any oxygen in case the flakey methane jets in the high school lab went out. (Carbon dioxide is heavier than oxygen, so it’ll stay in the tube and force the oxygen out.) If the jets did go out with oxygen still in the tube, then I’d be standing at the open end of a pipe bomb because the flame would’ve backed into the pipe and ignited all the methane inside. Without the oxygen, there would be no explosion…just a slow burn off of the remaining methane.
In order to test this, I got a bunch of dry ice from the chemistry supply at NDSU. I filled a couple of soup thermoses and brought it to the high school. We tested things out, and our first test went fairly well.
As I was leaving the school, I was walking toward a teacher in the hallway. I was about to smile at him when I heard a huge “BANG!” I stood there, stunned, and a second later realized I had a really bad pain in my side. The teacher, who a second ago was smiling at me, came running at me. And he looked very angry. He started yelling at me, and I couldn’t understand what was going on.
I looked down while he’s angrily asking me questions, only to realize that he was angry because I was the source of the huge noise I’d just heard. I saw one of the thermoses, which had formerly been under my arm, had blown off the bottom and was laying in pieces on the floor. The pain I’d felt had been the thermos ejecting itself from my grasp.
Despite all my efforts to avoid being blown up by a pipe bomb, I’d managed to make a small explosive device anyway. I’d forgotten the ideal gas law…and over the past couple hours, it appeared that pretty much all of the dry ice had sublimated. A thermos full of solid dry ice turning to gas was going to create an extremely large amount of pressure.
I finally explained to the teacher that I wasn’t a student trying to blow up the school, despite the fact that I apparently looked young enough to be a student (at 28?!) and was standing in front of the administrative offices when the incident occurred. I explained who I was and what was going on…and once he realized I was half in a state of shock, he started helping me to clean up my thermos pieces.
And people wonder why I don’t want to be an experimentalist.
Friday Fun: Weird Al edition November 25, 2011
Posted by mareserinitatis in Friday Fun, physics.Tags: Donny Osmond, physics, Weird Al
2 comments
So you see Donny Osmond dancing around in front of the equation? Bonus points for those who can correctly identify it.
For the record, I adore Weird Al for putting an equation in a music video.
Undergrad physics inaccessible to women November 23, 2011
Posted by mareserinitatis in education, feminism, physics, teaching.Tags: education, gender equity, physics, problem solving, sexism
10 comments
I was very intrigued when this month’s Physics Today showed up in the mail. While scanning the table of contents, I noticed an article called, “Problems with problem sets.” The summary went on to say that the problem with undergrad physics courses is that they often use problems which require specific background knowledge. Men are more likely to be acquainted with this knowledge than women.
The gist of the is that many of the problems in physics texts assume knowledge of various areas like construction, meaning that more men than women will be acquainted with the problem set up. Many times, these problems will make reference to various tools or constructions without giving an explanation or picture to describe what’s going on. They assume the students will understand what is being asked without further explanation.
I guess I hadn’t run into this a whole lot as an undergrad, but I think I may be a special case. As a kid, I worked with woodworking tools because my dad was a carpenter. In fact, I regularly had to help out in the shop, so I got a lot of hands-on experience in building and working with tools.
On the other hand, I think that when I went back to school, I wasn’t afraid to ask questions. I’ve observed that there are a large number of students who don’t like to ask questions, especially among the youngest students.
It’s a very interesting premise. Obviously it didn’t deter me, but I can see how this would be very intimidating for young women. It would definitely make many of them feel like they didn’t have a good enough background to do the work. I’m glad that someone is paying attention to issues like these, and I hope professors will pay a lot more attention to the problem sets they give in the future.
Repost: Planet of Youth March 27, 2011
Posted by mareserinitatis in education, math, physics, science, teaching.Tags: acceleration, age, gravitation, physics, planets, velocity
2 comments
If you’ve ever wondered how old you are in Jupiter years, this is your chance to find out. All you need are the following: your age in earth days, the mass of sun and the distance between the planets and sun. And Math!
Note: The reason you are using variables for most of the project is so that you can use any planet you want. If you did this for each planet using numbers, you would have to do everything over for each planet. If you want to cheat and avoid the math (as well as get a more exact value), you can check out Your Age on Other Planets.
These are the variables we will be using:
G is called the gravitational constant (we’ll give you this later)
Ms is the mass of sun
Mp is the mass of the planet
A is the acceleration (how much it’s speed changes in time)
R is the distance of the planet from the sun
First use the following equations:
(1) 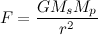
This is Newton’s Law of Gravitation.
This says that the force exerted on a planet is proportional to the mass of the planet, Mp, and the mass of the sun, Ms. It is inversely proportion to the distance between the planet and the sun, squared, or R2. If you increase the mass of the planet or the mass of the sun, the force will increase. On the other hand, the force will decrease if you increase the distance between the two. However, the decrease isn’t linear – that is, it doesn’t decrease a fixed amount for a change in distance. It will change based on the square of the distance, faster than if the distance wasn’t squared.
(2) 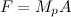
This is Newton’s Second Law
This equation states that the force on the planet is equal to its mass times its acceleration.
Both equation (1) and equation (2) are equal to the force. Set them as equal to each other (using the transitive property: if a=b and b=c, then a=c). Then solve for A.
Your result should show that the acceleration on the planet only depends on the mass of the sun and the distance between the planet and the sun. The acceleration isn’t affected by the mass of the planet!
Now we’ll give you another equation for A:
(3) 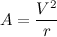
The is the acceleration of a circular path (the orbits of the planets are very nearly circular)
What this equation says is that the speed changes by a factor of the speed (V) squared over the distance between sun and the planet. If you ever want to get into Newtonian mechanics, you’ll run into this as a basic result for how speed and acceleration are related when an object moves in a circular path.
2. Use your two equations for A (the one above and your result from Exercise 1) and solve for V, your velocity (or speed).
3. Now that you have an equation for the velocity, you know how fast the planet is moving. Again, the speed of the planet has nothing to do with the planet’s mass: it is only affected by its distance from the sun. The farther from the sun that the planet is, the slower its speed.
Let’s figure out how far the planet has to travel to make one orbit around sun. If the path traveled is a circle, and the radius is R, what is the circumference of the circle? Set this formula equal to distance, D.
4. We know how far the planet has to travel around the sun and how fast it goes. Let’s figure out how long a year is on that planet. Since speed is distance over time (V=D/T), we can rewrite this. Solve for T.
5. Now substitute your equations for V and D into your formula for T. This will give you an equation for the length of the year.
6. Now let’s test our answer. First, figure how long is an earth year in seconds? (Hint: the number of days in an earth year is 365.25.) Your answer (and all future answers) should have four significant digits. The answer will be your Converted Answer.
7. Use your formula for T to figure out how many seconds are in an earth year. The value for π is 3.14159, G is 6.67•10-11 N•m2/kg2, the mass of the sun is 1.99•1030 kg, and the radius of the earth’s orbit is 1.50•1011 m. Your answer will be in seconds. This is your Calculated Answer.
8. Now figure out how accurate your calculation is. The formula to calculate percent error is 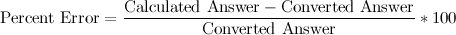
Your Percent Error should be less than 1%. If it is not, try to look for an error in your calculations.
9. Now use your formula to calculate the number of seconds in a year for your planet. Planetary radii are listed below.
Planet:______________________ Radius: _______________________________
Conversion Factor: __________________
10. How old are you in seconds? Multiply the number of seconds in an earth year, your Calculated Answer, by your age in years.
11. Now divide your age in seconds by the length of a year on your planet. How many years old are you on that planet?
12. Check your answer. You have been given a conversion factor for your planet. Divide your age by this number.
13. Now check how close your answers were. If your answer to 11 is your calculated answer, and your answer to 12 is your converted answer, use the equation in 8 to find your percent error.
Now ask someone older than you how old he or she is on Mercury.
——
This chart is for the instructor. Once the student has completed Exercises 1-8, they can get the information for their particular planet(s). The conversion factor is actually the number of earth years it take for that planet to make one revolution around the sun.
| Planet | Radius (m) | Conversion Factor |
| Mercury | 57.9•109 | 0.241 |
| Venus | 108•109 | 0.615 |
| Mars | 228•109 | 1.88 |
| Jupiter | 778•109 | 11.9 |
| Saturn | 1430•109 | 29.5 |
| Uranus | 2870•109 | 84.0 |
| Neptune | 4500•109 | 165 |
| Pluto | 5900•109 | 248 |
In case someone wants them, these are the answers to exercises 1-8.
1. 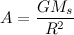
2. 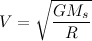
3. D=2πR
4. T=D/V
5. 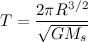
6. 31 557 600 seconds/year
7. 31 680 000 seconds/year
8. 0.39%
Things you don’t learn in physics December 3, 2010
Posted by mareserinitatis in electromagnetics, engineering, grad school, physics.Tags: engineering, physics, sea urchins, simulations
5 comments
One of my fondest memories of doing my masters degree was when I decided that I was going to prove out everything I’d been doing in my simulation work. This was in the days before we had our nice anechoic chamber.
I’d been designing antennas, so we took a cartful of antiquated equipment into the middle of a field, where we would ostensibly not have a lot of electrical interference and took a bunch of patterns.
When I got back in and was able to analyze my data, I realized that aside from the fact that my pattern seemed somewhat misaligned, I had something that looked like a sea urchin.
For all the effort of dragging that equipment around, it turned out that I’d managed to ruin things by having my cell phone in my pocket: it operates in approximately the same frequency range as my antennas, and the spikes were probably the phone attempting to communicate with a nearby tower.
That was the day that I learned how difficult it can be to go from equations or simulations to making something that actually works the way you want it to. When working on my undergrad in physics, I became adept at looking at analytical solutions at things, but I don’t think I got a really good handle on what they really meant by “ideal case” until I went into engineering.
Right now, I’m starting on a new project that involves building certain package components. I was discussing the project with the engineer who will be designing and building them (where I will be modeling and possibly testing them). We were discussing the electrical properties of one of the objects, and without thinking, I reached up, grabbed a textbook, and started discussing the theoretical behavior.
He made some comment about “that’s how grad students think”.
We have this problem. He is not sure what his yield will be, so he wants to make a whole bunch of variations on the design. However, each variation for me means a lot of time in terms of building my models and then computer time running them. I’d really like to keep my modeling work limited to about a dozen designs so that I’m not sitting there, still working on things next year at this time.
But when you build these devices, you don’t know what your tolerances are and how difficult it will be to make the device to spec. There may be problems with process, and so you may have to make a lot of changes to see what works.
It’s almost certain that it’s not going to operate the way it does in the simulations.
Sometimes it makes me think that modeling is a somewhat useless exercise. On the other hand, who has time to build and test hundreds of devices to see what works? (I mean…other than people like me and the other engineer.) At least with modeling, you have an idea of how it should work, and you can also tell if something is really amiss. Once you understand how your device deviates as it goes from simulation to testing, you may have something that makes it easy to predict what device will work for a particular application. Or maybe you can incorporate more and more of the real-life dynamics that affect your device into your model to make it increasingly realistic.
The scientist in me loves to come up with predictive models. It’s just that sometimes I feel like I’m trying to develop a perfectly spherical sea urchin.
My son is a nerd… November 17, 2010
Posted by mareserinitatis in physics, younger son.Tags: physics, younger son
2 comments
Not the older one, either.
Today an announcement about the APS April meeting showed up, complete with a poster advertising the event. The poster displayed a beautiful picture of the horsehead nebula. I was saying it was very nice but I wasn’t sure what I was going to do with it, and the younger boy jumped over and said, “I’ll take it!”
He taped the poster up in his room. Then he read the advertisement portion and informed me that he wanted to go to the APS meeting so he could learn about the papers.
Is it too early to hope my kid will grow up to be a physicist?

 I also blog at Engineer Blogs, home away from home to some of the best engineering blogs.
I also blog at Engineer Blogs, home away from home to some of the best engineering blogs.
My theory on the Big Bang Theory January 30, 2012
Posted by mareserinitatis in humor, physics, science, science fiction, societal commentary.Tags: Big Bang Theory, physics, stories, suspension of disbelief, TV
10 comments
I really don’t watch much TV, but I do own all of the Big Bang Theory that’s available on DVD. Most of my friends really enjoy it, too, and I have a theory why that is: I think that it’s one of the few TV shows that nerds can stand to watch because it is far more factually correct than most TV shows.
Most of the nerds I know are the ones who annoy everyone else at movies by making commentary throughout about the impossibility or improbability of what they’re witnessing. (In particular, my older son is this way. Of course, he also likes to tell you what’s going to happen next, so he’s been banned from speaking during movies.) Suspension of disbelief becomes a little harder when you’re faced with something you know cannot possibly happen.
I think this became obvious to me in where Sheldon was waxing (un)poetic about how great Isaac Newton was. Leonard made some comment meant in sarcasm, and Sheldon’s response was to say that Leonard disputed Newton’s claim that he invented calculus so Leonard wanted to put Leibniz at the top of the Christmas tree.
Most people who have no clue about calculus would probably laugh at this scene because Sheldon missed the point of the sarcasm. On the other hand, those of us who know anything about calculus might have been laughing because we knew exactly to what he was referring. And it made me ponder…would I want Newton at the top of my tree, or Leibniz? For the record, I would have been fine with Newton at the top of the tree because he did a lot more than invent calculus…but I still am glad for Leibniz’s wonderful notation. Either way, you couldn’t have just thrown any mathematician or physicist’s name out. It HAD to be Leibniz because the rivalry is so historic and well-known among mathophiles.
As I go through the show, I find little details like that a lot, and I really enjoy them. Whether or not I want to, I tend to pay attention to those points and letting them go is tough. Sometimes they even draw me in more than just the storyline does. In the episode where Sheldon is attempting to teach Penny physics, I kept thinking, “There’s better ways to explain that.” And when she was supposed to answer a question, it felt like sitting in a classroom and wanting to blurt out the answer.
It’s a real treat to watch a show that doesn’t use science as some sort of nifty backdrop to the story, where the science actually is important to the story or at least makes it more fun. And better yet, it still manages to entertain all the non-physicists out there, too.